harmonics pt. 0, the physics of

When, as in the practice of experimental improvisation, you are ‘allowed’ to do almost anything, there’s a distinct advantage in using a technique that limits your choices. Natural (open-string) harmonics fulfill the criteria of a limited palette, and, for those of us who came to improvisation via players like Derek Bailey, they, well, have the smell of a rich heritage.
Yet, after a cursory examination, this limited palette, on the contrary, turns out to be a large universe of possibilities. Possibilities that, let’s face it, traditional guitar pedagogy neglects, and for which traditional notions of technique are ineffectual.
So where does the aspiring guitarist start?
Before delving into the pedagogical and physiological aspects, I suggest they start with the physics of a vibrating string.

Note: To avoid confusion, I’m going to use ‘harmonic’ for the instrument playing technique and the resultant sound. I will use ‘overtone’ to talk about the mode of vibration.

There’s a familiar misconception that harmonics are ‘extra’ tones that somehow magically pop out when the string is played in a certain way. Harmonics are not ‘extra’ tones, but the result of the suppression of selected modes of vibration. In other words, harmonics are less than the unimpeded vibrating string.
A string will vibrate in a composite of several modes. A ideal (perfectly one-dimensional, evenly distributed mass, etc) string will vibrate in a composite of its fundamental and its overtones.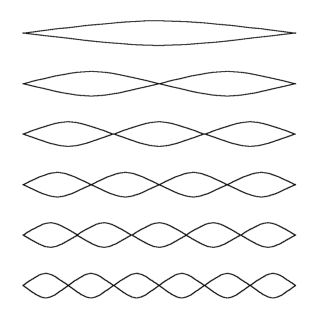
The above diagram represents the first six modes of vibration. I’ll refer to these as the 1st (or fundamental), 2nd, 3rd, etc. Note the integer sequence (1, 2, 3, 4, 5...) represented in the overtone series, and that each overtone effectively divides the string length (1/2, 1/3, 1/4, 1/5...). From this we can figure out where to semi-stop (lightly touch) the string to “play the harmonic.”
Let’s now see what happens when we do just that. As an example, if we semi-stop the string at the half-way point, the following modes of vibration are suppressed.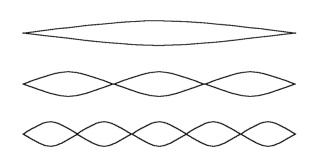
The supressed modes are, in this case, the odd ones (1st, 3rd, 5th...). All these are modes in which the string would have to move at the half-way point, but which it cannot since we have a finger pressed there.
The resultant vibration of the string is a composite of the following (2nd, 4th, 6th...).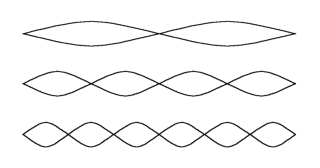
Looking at half the string, we’re back to that integer sequence (1, 2, 3, 4, 5...).
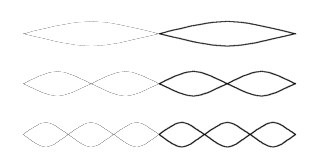In other words, we have effectively got a string that’s half the length, and a tone that’s twice the frequency (an octave higher in pitch). Also note that we have not added anything, we’ve merely masked out vibrations that would make the result sound like the fundamental.
I’ll leave it as an exercise to figure out how this applies when you semi-stop the string at other points (1/3, 2/3, 1/4, 3/4, 1/5, 2/5, 3/5, 4/5...).
Anyway, keep this picture in mind, and many of the problems in playing harmonics will be better addressed.

For more information checkout HyperPhysics’ articles on harmonics and sound and hearing.